RC Low pass filter

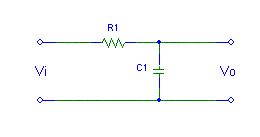
The impedance of R1= R and the complex impedance of C1 is given by and the output voltage is given by:

And the ratio between output and input voltage for this circuit is thus:

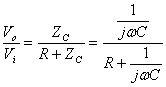
(1)

If we multiply the equation above with 1 or in this case with we finally get the transfer function:

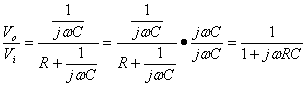
(2)

Now, any complex number can be written in a number of ways. One of the most common ways to write a given complex numkber C is: . This is actually a vector in O(0,0) with a certain length and a certain angle. The Modulo of the complex number C is the length, while the Argument of of the complex number C is the angle of the vector.

The Modulo is given by:

(3)

And the Argument is

(4)

We can now write the transfer function as given in (2) in the notation as given above.

(5)

With the result of (5) we can write the transfer function (2) a complex number C and we can calculate the Modulo and the Argument from it. The Modulo is given as:

And finally:

(6)

We can plot the results from the function above in graph:


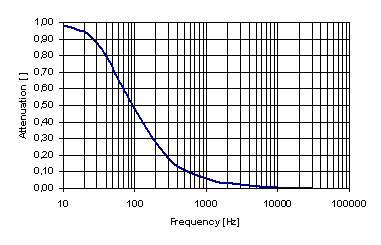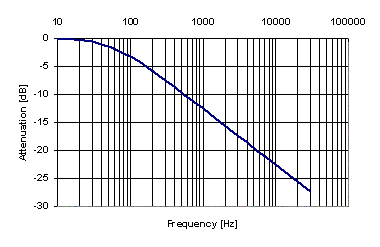Transfer function of a single stage RC filter.	Transfer function of a single stage RC filter, log.

The argument can be calculated as follows:

And finally:

(7)

We can plot the results from the function above in graph:


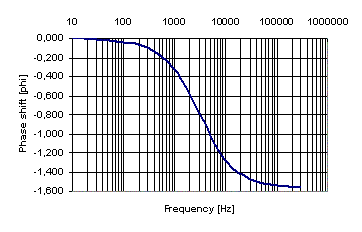Transfer function of a single stage RC filter.	Transfer function of a single stage RC filter, log.