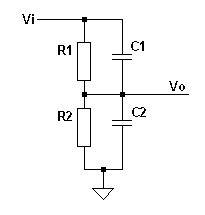
An attenuation network is often used in devices like a (digital) voltmeter, in oscillopscopes, etc. It offers the possibility to expand the input range of the measurement tool and thus makes it more versatile. Usually the attenuation network is build with a couple of resistor as shown in fig. 1. If the input resistance of the rest of devices is considered indefintie (as for example with a fet) the voltage is Vo=Vi*R1/(R1+R2). This works very well with DC-voltages.
However, with AC-voltages, things are not quit that simple. There are parasitic capicitances that ruins this simple setup. Figure 2 shows what is happening. For a DC-voltage this setup still works. However, with an AC-voltage it now becomes different. The total resistance is now the parallel of the resistor and the capacitance and is thus lower. The meter will thus show a lower reading and the accuracy of the instrument so carefully constructed is down the drain....
However, this can easily solved by adding some more capacitors. Yes, you read it correct even more capacitors!
In the network on the left, the well-known Wien network is shown. The impedance of the resistor is ![]() and of the condenser is
and of the condenser is ![]() and where
and where ![]() .
.
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc
|
| (1) |
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc
|
| (2) |
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc
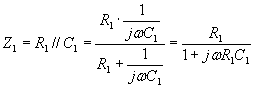
| (3) |
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc

| (4) |
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc

| (5) |
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc
|
| (6) |
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc
|
| (7) |
This circuit can be simplified to the circuit on the right. In this network Z1 is the sum of R and Zc
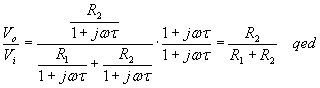
| (8) |